Alpa: Automating inter-and {Intra-Operator} parallelism for distributed deep learning
简介
Alpa 是第一个端到端可以生成并行执行计划的系统。这里的并行主要指 intra-op 和 inter-op 级的并行,intro-op 即我们所说的算子并行、数据并行(需要划分张量),inter-op 即我们说的流水线并行(不需要划分张量)。图 (e) 展示了 Alpa 如何分解模型训练的并行层次。
实现采用 JAX 作为前端,XLA 作为后端,编译步骤使用了 JAX 和 XLA 的 IR,分布式使用了 Ray,使用 XLA 来执行计算图,NCCL 来通信。
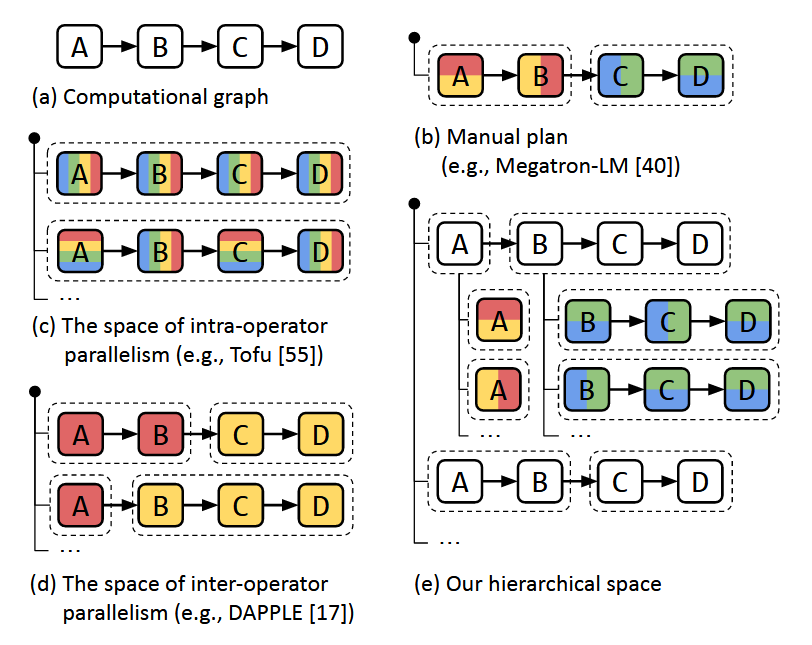
Alpa 将优化问题分解为两部分:intra-op 级的优化和 inter-op 级的优化。由于 inter-op 级依赖 intra-op 级的 cost 估算,所以文章先描述前者。优化流程(文章叫做compilation pass)如图:
- inter-op pass,主要计算出最优的 pipeline parallism 的划分方法。假定模型可以划分为层次结构,如何找到最优方法划分出 stage ,最大化利用 device。每个 stage 需要计算其 intra-op pass 优化的结果(也即是使用文章中的 intra-op pass 估算出当前 stage 的时间)。
- intra-op pass,计算出当前 stage 最优的并行方法(各种并行算法的最优组合)。
- runtime orchestration,这一步骤主要优化通信,看下通信原语是否可以利用更便宜的方式(举个🌰️,跨机器广播,可以采用广播到一个机器,然后机器内节点通信方式)。
limitations
这里摘几点重要的:
- pipeline parallism 的通信没有考虑,作者解释 cross-stage 的通信量很小所以不考虑,如果真要考虑也可以使用同样的解法(sure, 动态规划里面加上一个估算即可)。
- 没有考虑 overlap 通信和计算。
- 只支持静态计算图,所有 tensor 大小在编译时即确定。
intro-op pass
计算图中,节点为算子,边为张量(分布式计算时,需要通信)。找到下面公式的最优解:
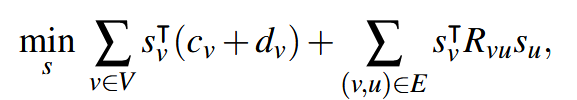
第一部分为算子计算和通信开销,第二部分为算子和算子之间的通信开销(例如使用张量并行这时可能需要 reduce 了,当然也可能不需要,取决于使用的算子)。
预估方式:通信开销直接算通信量 / 带宽。计算开销直接忽略(小矩阵计算快可以忽略,大矩阵认为开销一样)。为了简化计算图,把一些没有计算量的算子直接合并了(可能直接忽略掉了)。
这里直接使用的整数线性规划算法求解。
inter-op pass
inter-op 的优化即 pipeline parallism 的优化,找到最佳的分配方法(如何把模型划分为stage,然后对应的stage放到哪些设备上)。
找到下面公式最优解:
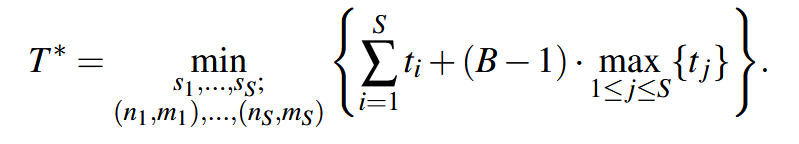
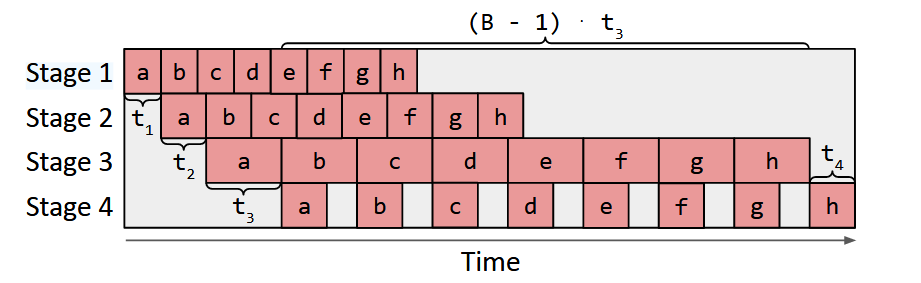
总时间如 timeline 图所示,等于第一部分(若干个stage的前向和后向时间总合,Alpa不处理特殊反向传播计算图)+ 第二部分(最长的stage耗时 * (B-1))其中 B 为一个任务划分的个数(流水线中的 micro-batch)。t 为 intra-op 计算预估的结果。
这部分求解直接采用动态规划,先枚举最大时间:
文章提及的trick: Mesh device 只使用2种方式(保证划分最优),超过内存限制认为执行时间♾️。
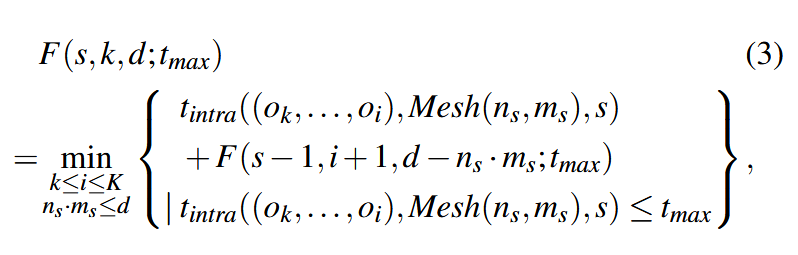
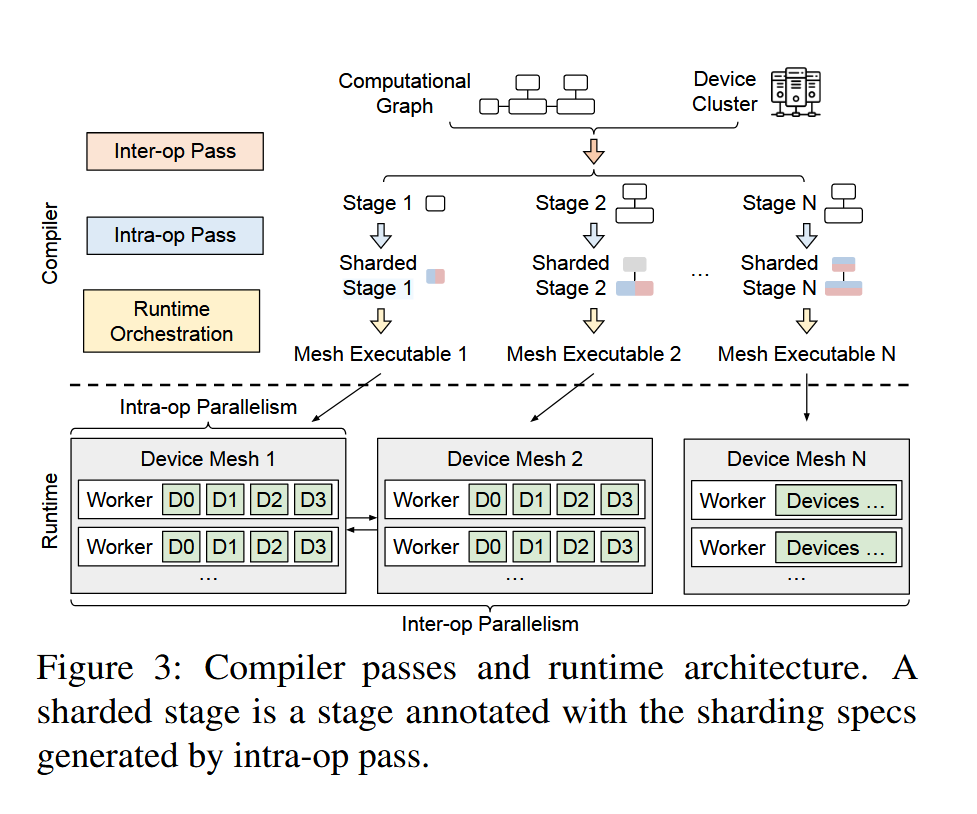
runtime orchestration
这一部分主要优化通信,如图所示:mesh 内通信带宽大,mesh 间通信带宽小的场景如何保证通信时延小。check 是否有机会在同 mesh 中 replicate 数据而非 copy from cross-mesh.